Reflection #1: Unit Q

#1. What does it actually mean to verify a trig identity?

You show that the Pythagorean Theorem is correctly used in the triangles to find sine and co-secant, cosine and secant, and tangent and cotangent. For example,  if you are given sine=3/5 you know that cosine must equal 4/5. You get the 4 from the Pythagorean Theorem 3^2+b^2=5^2; b=4. Meanwhile, you show that you get the the 5 as the denominator as well as the c value in the Pythagorean Theorem because we know that sine is S-O-H, opposite/hypotenuse and cosine is C-A-H, adjacent/hypotenuse. Also, tangent is T-O-A, opposite/adjacent. ( Soh cah toa is use for right triangles only).

To better visualize the concept, please take a look at the images below:





http://www.mathwarehouse.com/trigonometry/images/sohcohtoa/sohcahtoa-all.png





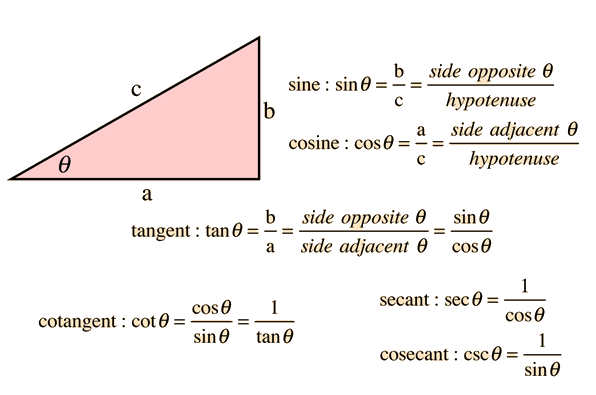
http://hyperphysics.phy-astr.gsu.edu/hbase/imgmth/ttrig.gif



#2. What tricks and tips have you found helpful?

I found that knowing the trig identities out of the top of your head was really helpful. However, there is no shame in not being able to memorize them quick enough or at all. I do think is better if you do know them because then you are more familiar with the concept and you have a better idea of how to get where you want to get. I suggest you do Mrs. Kirch's blog posts with thoughtfulness and to practice as much as possible and to ask questions. I also remember having problems in which knowing how to factor pretty good will help you a lot in simplifying or verifying.





#3. Explain your thought process and steps you take in verifying a trig function. Do not speak in specific manners, but speak in general terms of what you would do no matter what they give you.

My thought process would be:

• can I substitute an identity?
• can I use ZPP?
• are the numbers in the problem familiar with unit circle numbers?
• do I have to Square anything?
• does it deal with fractions?

1. - 

do I know how to deal with fractions(ex. when you multiply a fraction you do not have to have like terms!)

BQ #4: Unit T Concept 3: Graphing tangent and cotangent

To understand why "normal" tangent graph is uphill, but "normal" cotangent graph is downhill, you must understand how each is applied in the unit circle. Tangent is sine over cosine. Cosine is 0 at 1/2 radian and at -1/2 radian so this determines where the asymptotes are placed. According to where the asymptotes is how the graph is formed. For instance -1/2 radian comes first then 1/2 radian and quadrant 4 and 1 are in between. In quadrant 4 tangent is negative so it goes below and in quadrant 1 tangent is positive so it goes above.

Cotangent is just above, below because the asymptotes end up in different places since cotangent is cosine over sine and sine is 0 in 0 radian and 1 radian.

BQ #3: Unit T Concept 1-3: Graphing sine, cosine, cosecant, secant, tangent, cotangent

 


The above pictures show the relation between sine and cosine with all the other trig function graphs. Notice that sine and cosine graphs are similar in the way they swingle continuously. In contrast to the other graphs, which obtain asymptotes and do not continue in the way that sine and cosine do. Those rest of the trig functions that have asymptotes go on forever in a vertical way. In Mrs. Kirch's words, those trig function graphs require us to raise our pencil to continue to outline the rest of the graph.




You are recommended to go to desmos.com in order to have a full experience on how different values affect the graph.

BQ #5: Unit T Concept 1-3: Graphing sine, cosine, cosecant, secant, tangent and cotangent

Sine and cosine do not have asymptotes, meanwhile all the other trig functions have asymptotes. But, why? Remember that an asymptote forms when there is an undefined ratio/fraction. This means that there is a number divided by 0.
This is based on the trig function's ratios. Sine and cosine have ratios of y/r and x/r. "r" always equals to one in the unit circle so we can be sure that the ratio will never be undefined.
Meanwhile, the ratios for all the other trig functions have a denominator, not of r=1, but of either y or x values, which could happen to be values of 0.

BQ #2: Unit T Concept 1-3: graphing sine, cosine, secant, cosecant, tangent, and cotangent

Trig Graphs relate to the Unit Circle. We must consider the fact that in trig graphs, the Unit circle is expanded into a line form, instead of a circle form, in order to make sense in a graph.

*A period means the graph goes through one cycle while covering certain radian units on the graph. An amplitude are half the distance between the highest and lowest point of the graph.

*Periods.

For instance, sine, cosine, cosecant, and secant have a period of 2 radians. This is because it contains a 4 part repeating unit all the the way around the unit circle (360 degrees=2 radians). This is shown in the unit circle when we look at the pattern of where the sine and cosine are positive and negative.
Sine is positive on Quadrant I and II and negative on Quadrant III and IV. The pattern is positive positive negative negative. And it continues, but we must realize we had to go all around the unit circle in order to continue the pattern. The same with cosine, whose pattern is pattern is positive negative negative positive. The pattern continues but only have we went around the unit circle. Again, around the circle means it is 2 radians.

In contrast with tangent and cotangent, which have a period of only 1 radian. This is because they only have a 2 part repeating unit which just reaches half way through the unit circle at 180 degrees=1 radian until it repeats again. The pattern is positive negative positive negative all around the unit circle. There was one repetition in pattern so the pattern continues every 1 radian.

*Amplitudes

Sine and cosine have amplitudes because they are the ones with the restriction: -1<sine or cosine<1. This means that their highest point is 1 and its lowest point is -1. Relating to the unit circle, we know that the lowest it goes it to -1 and the highest it goes is to one (remember a unit circle has a unit of 1 all around) The sine an cosine ratios are y/r and x/r. The highest the y and x values could be is 1 and the lowest they can be is -1. ("r" is the ration equals to one).
The other trig functions instead go up forever or down forever because they do not have restrictions.