Special Right Triangles and the Unit Circle!
Heading for this Section Inquiry Activity Summary:
For the activity, we labeled the special right triangles.
For the 30 degrees triangle (which is the short one because it has the longer side down and the shorter side as its height) the hypotenuse/radius = r = 2x = 1 (because we are focusing on the Unit Circle which we know has a radius of 1). The short side (height) = y = x = 1/2, and this is because we divided r by 2x to make it equal 1 so we must also divide x by 2x to give it a value which is 1/2. the bottom side is x = x times radical 3 = radical 3 divided by 2. Given this information, we can also figure out the ordered pairs of this triangle assuming it is drawn out in the first quadrant of a graph. The point where the 30 degrees angles lies will of course be (0,0). Going to the next point lying on the x-axis, the ordered pair would be (radical 3 divided by 2 (x), 0). And the point lying above would be (radical 3 over 2(x), 1/2(y)).
For the 30 degrees triangle (which is the short one because it has the longer side down and the shorter side as its height) the hypotenuse/radius = r = 2x = 1 (because we are focusing on the Unit Circle which we know has a radius of 1). The short side (height) = y = x = 1/2, and this is because we divided r by 2x to make it equal 1 so we must also divide x by 2x to give it a value which is 1/2. the bottom side is x = x times radical 3 = radical 3 divided by 2. Given this information, we can also figure out the ordered pairs of this triangle assuming it is drawn out in the first quadrant of a graph. The point where the 30 degrees angles lies will of course be (0,0). Going to the next point lying on the x-axis, the ordered pair would be (radical 3 divided by 2 (x), 0). And the point lying above would be (radical 3 over 2(x), 1/2(y)).
http://00.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_30.gi
f
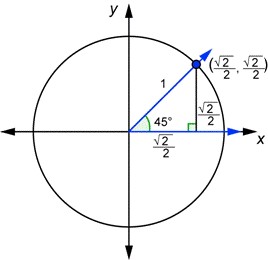
For the 45 degrees angle the values change, except the r remains = to 1. However, you must know that we got the value of 1 by dividing x radical 2 by x radical 2 because 45 degrees has different rule,according to the Special Right Triangle rules, the hypotenuse is x radical 2. not 2x like in the 30 degrees angles. The value for x and y are the same because they are the same length according to the rules of SRT. This value is radical 2 over 2 (let us set the y and x values as both x and they both become radical 2 over 2 when we divided the x by the hypotenuse value of x radical 2). The point where the 45 degrees lies will of course also be (0,0). Going to the next point lying on the x-axis, the ordered pair would be (radical 2 over 2 (x),0). And the point lying above would be (radical 2 over 2 (x), radical 2 over 2 (y)).
 |
http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U19_L1_T3_text_final_3_files/image036.gif
For the 60 degrees angle it is very similar to the 30 degrees angle. Just like the angles switch from where there were lying (as in the 30 degrees is no longer on the vertex point of the graph, instead now it is the 60 degrees angle opening), the values will switch too. This just means that x = 1/2 now and y = radical 3 over 2. r will continue to = 1. Meanwhile, the point where the 60 degrees angle lies now will of course be (0,0). The point lying on the x axis will be (1/2 (x), 0). And the point lying above would be (1/2 (x),radical 3 over 2 (y)).
http://00.edu-cdn.com/files/static/learningexpressllc/9781576855966/The_Unit_Circle_13.gif
This activity helped me to derive from the Unit Circle because I got a better understanding of where all the important values in the Unit Circle came from instead of just accepting them without expanded knowledge. Now I get a better sense of why and how we must learn many certain things in order for us to learn and understand others. This activity helped me have a better view of the 30, 45, and 60 degrees angles and fully comprehend the patterns that go along with them.
The triangles in this activity were all in the first quadrant but they may also lie on the second, third, and fourth quadrant, and refer to the degrees that they represent as reference angles. The number values of x and y do not necessarily change. Nevertheless, when we go from the first quadrant to the second one we will make sure that all the x values of each ordered pair of each angle are negative since the triangle is on the quadrant where the x-axis is negative while the y-axis is still going positive. On the third quadrant both the x and y values become negative and on the fourth quadrant only the y value becomes negative.
The below picture will give an example of how the 30, 60, and 45 degrees angles would look like in the quadrants II, III, and IV.
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjBOzfx3dUOBGPrCKd12aLaE85rhswxJHDtn_zO-5usBtImcuEhiPG66Uo7w_FibbJWWa0Du17esK5BaD-Cw14-FEgOpdfDdDNrc6k1yZJr27s_88FRNv7t55RSrkjIK12HwCRyrb4OfUc/s1600/012.
The coolest thing I learned from this activity was that you can find the ordered pairs of those points of a unit circle. I never thought you can actually look at a point in a curved circle and know its ordered pair (like actual x and y values!)
This activity will help me in the unit because I will have a complete understanding of where and how to get the values of certain points in the unit circle. I will therefore, understand the sine, cosine, and tangent better since they have to do a lot with these angles and ordered pairs.
Something I never realized before about special right triangles and the unit circle is that the sides of the triangle are measured x and y for a purpose of showing us the ordered pair, I literally thought they were labeled like that just because. I also did not realize the connection between the SOH CAH TOA and the unit circle but now the abbreviations make actual sense.
The below picture will give an example of how the 30, 60, and 45 degrees angles would look like in the quadrants II, III, and IV.
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjBOzfx3dUOBGPrCKd12aLaE85rhswxJHDtn_zO-5usBtImcuEhiPG66Uo7w_FibbJWWa0Du17esK5BaD-Cw14-FEgOpdfDdDNrc6k1yZJr27s_88FRNv7t55RSrkjIK12HwCRyrb4OfUc/s1600/012.
The coolest thing I learned from this activity was that you can find the ordered pairs of those points of a unit circle. I never thought you can actually look at a point in a curved circle and know its ordered pair (like actual x and y values!)
This activity will help me in the unit because I will have a complete understanding of where and how to get the values of certain points in the unit circle. I will therefore, understand the sine, cosine, and tangent better since they have to do a lot with these angles and ordered pairs.
Something I never realized before about special right triangles and the unit circle is that the sides of the triangle are measured x and y for a purpose of showing us the ordered pair, I literally thought they were labeled like that just because. I also did not realize the connection between the SOH CAH TOA and the unit circle but now the abbreviations make actual sense.
The Unit Circle at It's fullest!
http://t3.gstatic.com/images?q=tbn:ANd9GcR_fq7L0KBbyBoR514RtTD7Gf4NwC2FxBCPY-8S2EgBpovRuFj_:alvalxy.wikispaces.com/file/view/%25E6%259C%25AA%25E5%2591%25BD%25E5%2590%258D.jpg/306597904/%25E6%259C%25AA%25E5%2591%25BD%25E5%2590%258D.jpg
